Technology – FormuLens

Lens design publication

We presented a paper describing some of the core ideas behind our lens design algorithm in San Diego at the SPIE Current Developments in Lens Design and Optical Engineering.

(more…)

FormuLens Enterprise Operations (FormuLens Ops) is a cloud-based system of tools for giving businesses direct control over multiple lens designs and manufacturing labs. With FormuLensOps, businesses may configure the LDS (lens design software) options available to a lab or ECP by adding and removing available lens design options, adjusting and renaming those lens design options, and viewing production information and individual job performance. Businesses may add accounts for labs or ECP’s, as well as view and configure the manufacture settings used by each.

FormuLens Ops consists of multiple tools: LabOps, DesignOps, and DataOps, each with several capabilities.

(more…)

LifeForm Progressive Design

Lenses individually tailored to lifestyle

Our LifeForm progressive addition lens design can be viewed as a set of 14 different designs which target different usage priorities (including balanced options, for general use), while still providing full progressive functionality. The ideal lens can be selected in seconds using a simple 3-question survey which is summarized in the table below (further detail after the table).

Alternatively, a practitioner who wishes to limit offerings a small set of options can use the table to select those options.

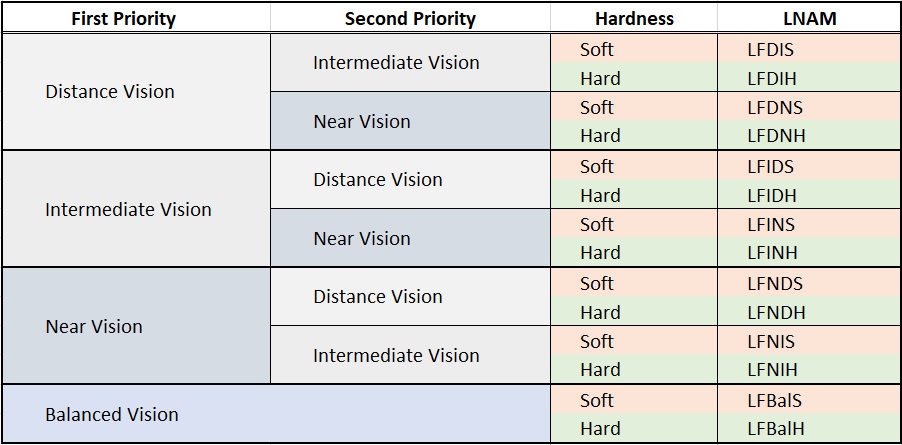
Preferences here boil down to having a larger region of clear viewing in the corresponding region of the lens (see Progressive Addition Lens Anatomy):

Distance vision – preference for outside use, such as driving, sports, etc.
Intermediate vision – preference for viewing in the channel, for better vision at each point across the entire range of viewing distances.
Near vision – preference for reading and close viewing.
Balanced – the best all-around design.

After the first priority is selected, a second priority can be chosen, for which of the remaining viewing zones should be emphasized.

Finally the LifeForm design has hard and soft options for every lifestyle option:

Hard designs – for experienced progressive wearers, those who adapt easily, and those who are otherwise not concerned not swim.
Soft designs – for beginning progressive wearers or those who have difficulty adapting. Adaptation is greatly improved at a cost of reduced viewing zone sizes.

Currently available in 18mm fitting height, all materials and physically-possible powers, with more frame options to come (and more design variations available for those who want it).

Please contact us at info@formulens.com for more info or to try it out.

SimuLens base functions

We have a new webpage explaining the basic functionality in SimuLens for simulating lenses a variety of ways.

gazing through a lens...

Click here to check it out.

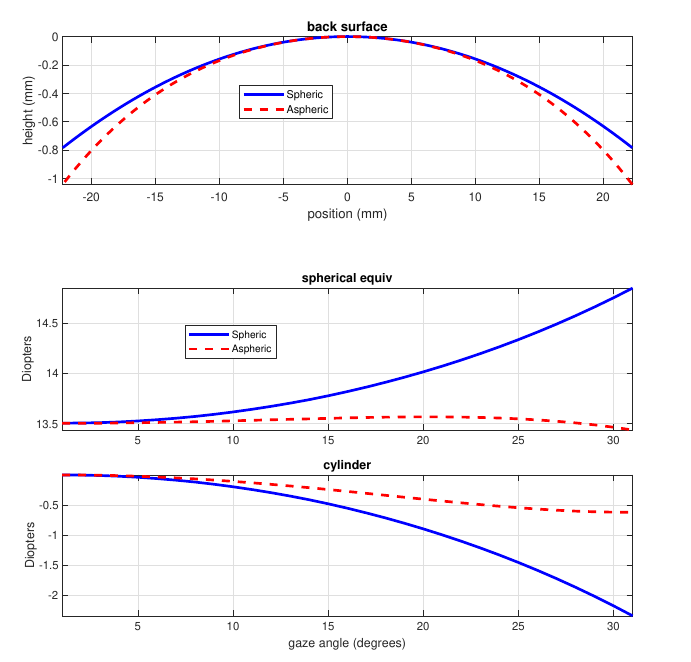
Aspheric Back Surface Designs

For high power single-vision lenses, significant improvement can be achieved with freeform lenses, even with spheric blanks. The following plots describe the performance for a surface optimized for a +13 Diopter prescription with CR-39 and a spheric blank.

(more…)

Small Lab LDS Software

FormuLens provides a minimal but fully-functional Lens Design Software (LDS) interface for ECP’s with their own generator and small labs, who don’t wish to purchase an expensive Lab Management Systems (LMS).

(more…)

Higher-order wavefront correction

With completely custom lens surfaces comes the opportunity to try and address higher order aberrations. The changing gaze angle of the eye during normal vision makes correction difficult in general use. However, researchers have claimed some improvements in vision using aspheric designs. Further, vision is a very active process, wherein eye movements are undertaken to improve understanding of the current scene. This suggests that the eye might discover and utilize a special high-order correction zone.

FormuLens provides the ability to incorporate various types of high-order corrections in freeform lenses.

Progressive Addition Lens Anatomy

With digital lens surfacing (a.k.a freeform) one or both surfaces of a lens can be completely specified by the Lens Design System (LDS). For example the LDS can provide a height map, giving points on a grid of some chosen spacing. This surface will be produced with very high accuracy by the generator.

The optical performance of a freeform lens when used in spectacles, is difficult to predict. Either the lens must be manufactured and analyzed with a complex apparatus that can measure optical properties for a range of realistic view directions, or the lens must be simulated computationally using sophisticated ray-tracing algorithms.

(more…)

Fast & Robust Wavefront Sensing

Rapidly rising levels of myopia, particularly in the developing world, have led to an increased need for inexpensive and automated approaches to optometry. A simple and robust technique is provided for estimating major ophthalmic aberrations using a gradient-based wavefront sensor. The approach is based on the use of numerical calculations to produce diverse combinations of phase components, followed by Fourier transforms to calculate the coefficients. The approach does not utilize phase unwrapping nor iterative solution of inverse problems. This makes the method very fast and tolerant to image artifacts, which do not need to be detected and masked or interpolated as is needed in other techniques. These features make it a promising algorithm on which to base low-cost devices for applications that may have limited access to expert maintenance and operation.

Dillon K; “Fast and robust estimation of ophthalmic wavefront aberrations“. J. Biomed. Opt. 0001;21(12):121511. doi:10.1117/1.JBO.21.12.121511. (pdf)

Custom Generic Progressive Lens

The FormuLens Custom Generic PAL (Progressive Addition Lens) is a single product which can be adjusted through a wide range of performance requirements. With adjustable fitting heights from 12 to 22 mm, and “hardness” ranging between the extremes offered by designs from major vendors, and everything in between. The design is optimized computationally using our lens design system SimPAL for a dense grid of setting combinations.

(more…)

« Previous